[python] 스택(Stack)과 DFS

 

파이썬에서 스택과 큐는 모두 리스트로 구현한다.

 

 

 

스택(Stack) 자료구조

 

후입 선출 자료구조. ex) 총의 탄창, 급식판 등

 

 

스택은 뭔가를 쌓는다는 이미지를 떠올리면 된다.

 

파이썬에선 리스트를 활용하여 스택을 구현할 건데, 파이썬 리스트를 90도 회전해서 돌린 이미지를 상상하면 된다.

 

 

 

스택은 나중에 들어온 데이터가 먼저 빠져나가게 된다.

 

중요한 점은, 데이터의 삽입과 추출이 모두 리스트의 뒷부분에서 일어난다는 것이다.

 

신규 데이터의 삽입은 append()를 활용하며 데이터의 추출은 pop()을 활용하여 메서드로 자연스럽게 스택 자료구조를 구현할 수 있다.

 

예시 코드로 구현해보겠다.

 

 

 

▶ 웹 서핑을 하다가 뒤로 가는 경우를 구현

visits = [] # 방문 기록지

#1. 처음으로 구글에 방문
visits.append('google') # ['google']

#2. 그 후 인스타에 방문
visits.append('instagram') # ['google', 'instagram']

#3. 그 다음 페이스북에 방문
visits.append('facebook') # ['google', 'instagram', 'facebook']

# 4. 뒤로가기 버튼을 누름
visits.pop()
print(visits) # ['google', 'instagram'] => 다시 인스타그램 페이지로 돌아옴

 

 

 

 

 

 

▶ class를 활용하여 스택을 직접적으로 구현하는 방식을 사용해보겠다.

 

class Stack:
    def __init__(self, n):
        self.top = -1
        self.stack = [0] * n

    def push(self, data):
        if self.top == len(self.stack) - 1:
            return None
        self.top += 1
        self.stack[self.top] = data

    def pop(self):
        if self.top == -1:
            return None
        self.top -= 1
        return self.stack[self.top + 1]

    def get_stack(self):
        if self.top == -1:
            return 'Stack is empty'
        return self.stack[:self.top + 1]

my_stack = Stack(10)
my_stack.push('alex')
my_stack.push('sungmin')
print(my_stack.get_stack())  # 전체 스택 내용 확인
print(my_stack.pop())
print(my_stack.get_stack())  # 팝 이후 전체 스택 내용 확인

 

 

 

class 코드 분석

 

 

 

class Stack:

    def __init__(self, n):

        self.top = -1

        self.stack = [0] * n

 

• __init__ 부분은 스택 초기화
• self.top은 스택의 최상단 인덱스를 나태며 초기값은 -1로 스택이 비어있음을 의미한다.
• self.stack은 크기가 n인 리스트로, 스택을 저장할 공간이다.

 

 

 

def push(self, data):

        if self.top == len(self.stack) - 1:

            return None

        self.top += 1

        self.stack[self.top] = data

 

• push는 스택에 데이터를 추가하는 메서드이다.
• 스택이 가득 찬 경우(None을 반환) 데이터를 추가하지 않는다.
• push를 하면 스택의 최상단 인덱스를 증가시키고 데이터를 추가한다.

 

 

 

def pop(self):

        if self.top == -1:

            return None

        self.top -= 1

        return self.stack[self.top + 1]

 

• pop은 스택에서 데이터를 제거하고 그 데이터를 반환하는 메서드이다.
• 스택이 비어있는 경우(None을 반환) 데이터를 제거하지 않는다.
• pop을 하면 스택의 최상단 데이터를 반환하고 인덱스를 감소시킨다.

 

 

 

def get_stack(self):

        if self.top == -1:

            return 'Stack is empty'

        return self.stack[:self.top + 1]

 

• get_stack 메서드는 스택의 현재 상태를 반환하는 메서드이다.
• 스택이 비어있는 경우엔 stack is empty라는 문구를 반환한다.
• get_stack을 하면 스택의 최상단까지의 내용을 리스트로 반환한다.

 

 

 

my_stack = Stack(10)

my_stack.push('alex')

my_stack.push('sungmin')

print(my_stack.get_stack())  # 전체 스택 내용 확인

print(my_stack.pop())

print(my_stack.get_stack())

 

• Stack(10)을 통해 크기가 10인 스택을 생성한다.
• push를 하여 스택에 'alex'를 추가한다.
• 스택에 'sungmin'을 추가한다.
• print(my_stack.get_stack())을 하여 스택의 현재 상태를 출력한다.
• print(my_stack.pop())을 하여 스택에서 최상단 데이터를 제거하고 반환한다.
• print(my_stack.get_stack())을 하여 pop 이후의 스택의 현재 상태를 출력한다.

 

 

 

▶ 결과값

 

 

 

 

 

 

 

 

 

 

DFS (Depth First Search, 깊이 우선 탐색)

 

Stack을 활용하여 DFS를 구현할 수 있다.

 

 

 

 

먼저 DFS에 대해 간단히 소개하겠다.

 

DFS는 깊이 우선 탐색이라고 불리며 그래프 탐색 알고리즘 중 하나이다.

 

그래프의 모든 노드를 방문하는 방법인데, DFS는 스택 자료 구조를 사용하며, 재귀적으로 또는 명시적인 스택을 사용하여 구현할 수 있다.

 

 

 

 

DFS의 기본 개념

 

 

 

1. 시작점에서 출발 : DFS는 그래프의 특정 시작 노드에서 출발한다.

 

2. 한 방향으로 끝까지 탐색 : 한 노드에서 연결된 노드를 따라가며, 더 이상 연결할 수 없을 때까지 계속 깊이 탐색한다.

 

3. 백트래킹 : 더 이상 방문할 노드가 없으면, 이전 노드로 돌아가서 다른 방향으로 탐색을 계속한다.

 

4. 모든 노드를 방문할 때까지 반복 : 이 과정을 통해 모든 노드를 방문할 때까지 탐색을 반복한다.

 

 

 

 

DFS의 동작 방식

DFS의 동작 순서를 분석해보자.

 

1. 시작 노드를 스택에 추가 : 시작 노드를 스택에 넣는다.

 

2. 스택에서 노드를 꺼내 방문 : 스택에서 노드를 하나 꺼내 방문한다. 이 노드를 방문했다고 표시한다.

 

3. 인접 노드를 스택에 추가 : 현재 노드와 연결된 모든 인접 노드 중 아직 방문하지 않은 노드를 스택에 추가한다.

 

4. 반복 : 스택이 비어 있지 않는 한 2번과 3번 방법을 반복한다.

 

 

 

 

예시

 

만약  이런 그래프(루프)가 있다고 하면 파이썬으로 어떻게 구현할 수 있을까?

 

먼저 이 동그란 포도알 같은 것들을 노드(Node) 혹은 정점(Vertex) 이라고 하며, 파란색 선은 간선(Edge) 이라고 부른다.

 

 

 

 

 

Stack을 왜 쓰는거고 이게 왜 깊이 우선 탐색인가?

 

방문 순서는 어떻게 될까 ?

 

노트에 적어봤다.

 

 

 

 

이렇게 빈 스택이 있다. 

 

 

 

 

 

먼저 1번 노드를 방문하고 방문한 노드로 빼버린다.

 

 

 

 

 

1번 노드를 뺀 후 2번과 3번 노드를 넣어준다.

 

 

 

 

 

3번 노드를 방문했으므로 빼주고 7번 노드를 넣어준다.

 

 

 

 

 

7번 노드를 빼주고 6번 노드를 넣어준다.

 

 

 

 

 

6번 노드를 빼주고 4번 노드와 5번 노드를 넣어준다.

 

 

 

 

 

5번 노드를 빼주고 나면 남은 노드는 스택에 담겨 있는 4와 2 뿐이다.

 

 

 

 

 

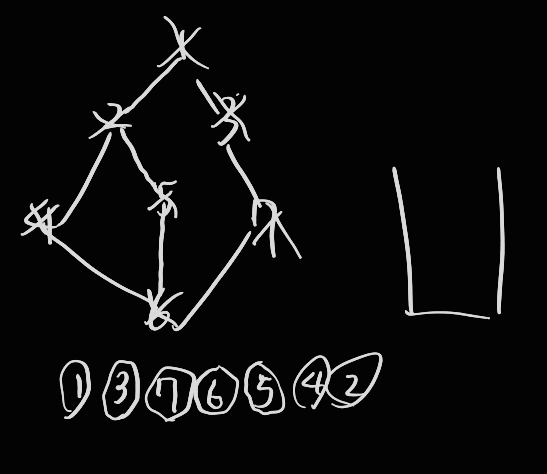
결과적으로 노드 방문 순서는 1 > 3 > 7 > 6 > 5 > 4 > 2 이렇게 된다.

 

 

 

 

 

 

이제 파이썬 코드로 정리해보자

 

 

 

 

 

def dfs(graph, start):
    visited = []
    stack = [start]

    while stack:
        node = stack.pop()
        if node not in visited:
            visited.append(node)
            for neighbor in (graph[node]):
                stack.append(neighbor)

    return visited

              

# 그래프 정의
graph = {
    1: [2, 3],  
    2: [4, 5],  
    3: [7],     
    4: [],     
    5: [],      
    6: [4, 5],      
    7: [6]      
}

# DFS 실행
result = dfs(graph, 1)
print(result)  # 출력: [1, 3, 7, 6, 5, 4, 2]

 

 

 

분석

 

 

# 그래프 정의

graph = {

    1: [2, 3], 

    2: [4, 5], 

    3: [7],     

    4: [],       

    5: [],       

    6: [4, 5], 

    7: [6]     #각각 자식 노드들의 정보를 보고 작성

}

 

1번 노드에서 시작하여  DFS를 수행하며 인접 노드를 방문한다.

 

 

 

 

DFS 구현

 

def dfs(graph, start):

    visited = []

    stack = [start]

    while stack:

        node = stack.pop()

        if node not in visited:

            visited.append(node)

            for neighbor in (graph[node]):

                stack.append(neighbor)

    return visited

 

 

 

DFS 함수의 작동 방식

 

 

1. stack을 사용하여 탐색할 노드 관리

 

2. stack에서 노드를 꺼내서 방문

 

3. 아직 방문하지 않은 경우, 노드를 visited 리스트에 추가

 

4. 현재 노드의 인접 노드를 스택에 추가

 

 

 

while stack:

• 역할: 스택이 비어있지 않은 동안 루프를 계속 실행한다.
• 조건: 스택에 방문할 노드가 남아있는지 확인한다.

 

 

node = stack.pop()

• 역할: 스택의 맨 위에 있는 노드를 꺼내서 node 변수에 저장한다.
• 효과: 스택은 후입선출(LIFO) 구조이므로, 가장 나중에 추가된 노드가 먼저 꺼내진다.

 

 

if node not in visited:

• 역할: 현재 노드가 아직 방문되지 않은 경우에만 아래 코드를 실행한다.
• 조건: 노드가 visited 리스트에 포함되어 있는지 확인한다.

 

 

visited.append(node)

• 역할: 현재 노드를 방문 목록에 추가한다.
• 효과: 노드를 방문했다고 기록하여, 다시 방문하지 않도록 한다.

 

 

for neighbor in graph[node]:

• 역할: 현재 노드의 모든 인접 노드(neighbor)를 순회한다.
• 효과: 각 인접 노드를 스택에 추가하여 나중에 방문할 수 있도록 준비한다.

 

 

stack.append(neighbor)

• 역할: 현재 노드의 인접 노드를 스택에 추가한다.
• 효과: 인접 노드들이 스택에 추가되므로, 나중에 방문할 수 있다. 스택은 후입선출(LIFO) 구조이기 때문에 나중에 추가된 인접 노드가 먼저 방문된다.

 

 

https://www.youtube.com/watch?v=_hxFgg7TLZQ

 

이 강의를 참고하면 좀 더 이해하기 쉬울 것이라 생각된다.